
Talföljder och cirklar: Algoritmer, geometri och mönster | 2 av 4
Lektionen handlar om hur algoritmer kan användas för att skapa geometriska mönster.
Användning av algoritmer i geometri
Några av de första uppgifterna datorer fick lösa när de uppfanns var att göra geometriska uträkningar. Eftersom datorer är så snabba på att räkna är de idag perfekta verktyg för att bearbeta ritningar, 3D-objekt och mycket annat som använder matematiska formler för geometri.
Men genom att rita utifrån matematiska formler kan en dator också skapa vackra mönster och konstverk. Varje bild en dator ritar i ett modernt spel är uppbyggt av 3D-objekt som sätts ihop, färgläggs och animeras. För att en dator ska veta hur ett av dessa mönster ska utformas och ritas upp behövs en programmerad kod som innehåller en eller flera algoritmer. Algoritmerna är datorns recept och bruksanvisning för att kunna skapa formerna.
Talföljder och algoritmer
En talföljd är en serie tal efter varandra. Talföljder kan ha mönster, och kan då uttryckas som algebraiska formler eller algoritmer. Treans multiplikationstabell är en talföljd som ser ut så här:
0 3 6 9 12 15 18 21 24 27 30
Det går snabbt och enkelt att se att det finns ett mönster i talföljden. Den gemensamma nämnaren är talet tre. Talföljden skulle kunna uttryckas i en ekvation (eller som en algoritm) på följande sätt:
x = n * 3
där ett villkor kan vara att: n är ett heltal mellan 0 och 10.
Inom programmering används ofta talföljder för att skapa flöden med hjälp av algoritmer.
Det binära systemet som datorer använder sig av använder en talföljd:
1, 2, 4, 8, 16, 32, 64, 128, 256, och så vidare.
Utgå från texten om talföljder och besvara frågorna.
- Vad är en talföljd?
- Kan du skriva talföljden för 5:ans multiplikationstabell?
- Kan du skapa en "ekvation" för att beskriva talföljden så att en dator skulle kunna använda den. Behöver du ange några villkor för datorn?
- Kan du beskriva algoritmen för talföljden som datorer använder?
Använd Scratch för att beräkna omkrets och area på en cirkel
Använd formeln för cirkelns omkrets och area.
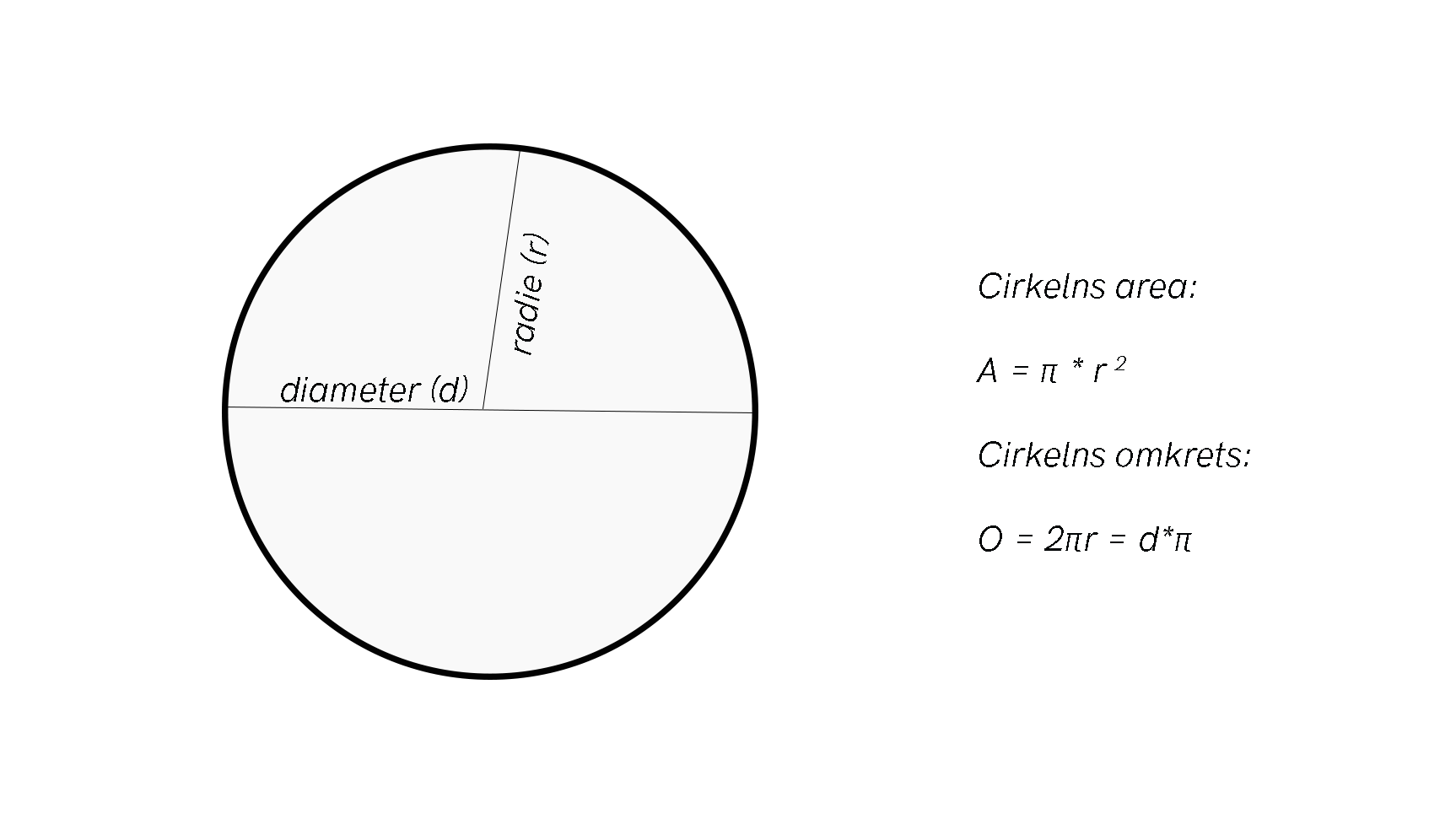
Arbeta med cirkelns area och Scratch
- Skriv formeln för cirkelns arean som en programmeringsalgoritm?
- Pröva Scratch projektet "Räkna ut omkrets och area på en cirkel"
3. Använd Scratchprojektet för att lägga in kod så du med hjälp av programmet automatiskt kan beräkna cirkelns omkrets, area och radie efter att du har ändrat storleken på cirkeln.
För läraren
Se lärarinstruktioner
Lektionens syfte
Lektionen syftar till att ge eleverna ökad förståelse för algoritmiska mönster och geometri inom matematik. Detta genom att analysera, modifiera och skapa algoritmer i Scratch för att samtidigt öva på att koda.
Förberedelser
En förutsättning för att göra denna övning är att eleverna har grundläggande kunskaper i hur det blockbaserade programmeringsverktyget Scratch funkar. Lär dina elever grunderna i Scratch genom att göra lektionsserien Scratch för nybörjare med dem. Då får eleverna lära sig verktyget genom att stegvis bygga ett spel.
Denna lektion förutsätter även att eleverna är bekanta med begreppet algoritmer. Låt eleverna undersöka begreppet genom att göra lektionen Undersök och diskutera sökalgoritmer. I första lektionen uppmanas eleverna att titta och ta del av följande film för att få en förståelse för hur matematik används i programmering:
Tänk på att det är viktigt att förmedla att programmering handlar om att prova, testa och göra om. Misstag och fel är nödvändigt för att kunna lösa problem. Prata gärna med eleverna om begreppet bugg. Förslagsvis genom att använda material från lektionen Buggar eller fel vid programmering.
Om Scratch
Scratch är ett verktyg där eleverna arbetar med programmering genom att använda block som sammanfattar kodsnuttar i ”vanlig” kod. Scratch är ett programmeringsverktyg för barn och unga som är framtaget vid det amerikanska universitetet MIT . Med Scratch kan du lära dig grunderna i programmering genom visuella block som byggs ihop likt legobitar för att skapa spel, animationer och enklare program.
Scratch finns på svenska och många andra språk. Det är helt gratis att använda. Om du använder inloggning är dock Scratch inte GDPR-kompatibelt. MIT har inte PuB-avtal och lagrar all sin data på servrar utanför EU. Det innebär att du som lärare behöver ta ställning till och informera dig hur du kan använda Scratch programvara på bästa sätt.
Om du undviker användarkonton som är kopplade till eleverna kan du arbeta med Scratch utan att vara inloggad. Du kan då spara ner projekten lokalt på datorn.
Genomförande
Titta på Scratch-projekten tillsammans med eleverna och låt dem sedan remixa dem för att skapa algoritmer som löser uppgifterna.
Se läroplanskoppling
Skolans uppdrag
Skolan ska bidra till att eleverna utvecklar förståelse för hur digitaliseringen påverkar individen och samhällets utveckling. Alla elever ska ges möjlighet att utveckla sin förmåga att använda digital teknik. De ska även ges möjlighet att utveckla ett kritiskt och ansvarsfullt förhållningssätt till digital teknik, för att kunna se möjligheter och förstå risker samt kunna värdera information.
Matematik
Syfte
Undervisningen i ämnet matematik ska syfta till att eleverna utvecklar kunskaper om matematik och matematikens användning i vardagen och inom olika ämnesområden. /.../Genom undervisningen ska eleverna ges förutsättningar att utveckla förtrogenhet med grundläggande matematiska begrepp och metoder och deras användbarhet. Vidare ska eleverna genom undervisningen ges möjligheter att utveckla kunskaper i att använda digitala verktyg och programmering för att kunna undersöka problemställningar och matematiska begrepp, göra beräkningar samt för att presentera och tolka data.
Centralt innehåll i ämnet matematik (åk 7-9)
Algebra
- Mönster i talföljder och geometriska mönster samt hur de konstrueras, beskrivs och uttrycks generellt.
- Programmering i visuell och textbaserad programmeringsmiljö. Hur algoritmer skapas, testas och förbättras vid programmering.
Geometri
- Geometriska objekt samt deras egenskaper och inbördes relationer. Konstruktion av geometriska objekt, såväl med som utan digitala verktyg.
- Metoder för beräkning av area, omkrets och volym hos geometriska objekt, samt enhetsbyten i samband med detta.
